GetCompress: compactando stacks raster para operar mais rápido sem perder o grid original

---

Eu estava lendo o artigo de Almaghrabi et al. (2024) sobre previsão multivariada de séries temporais de geração solar, usando fusão de dados em múltiplos. No meio da discussão, uma ideia prática ficou martelando, que no dia a dia quando temos dados grandes e heterogêneo, muitas vezes o gargalo não está no modelo, e sim em como representamos e movemos esse dado pelo pipeline. Isso me fez querer voltar a escrever aqui, e trazer uma visão de solução para um problema bem comum em geoprocessamento, como operar rasters gigantes sem desperdiçar memória e I/O com áreas vazias.

Quando um raster vai para produção, principalmente em escala nacional, o gargalo quase nunca é “falta de modelo”. Na prática, o que pesa é volume, I/O e desperdício de memória. Nós precisamos carregar um grid enorme para representar o território inteiro, mas boa parte dele não carrega informação útil, como mar, bordas, nodata e buracos de reamostragem.

A proposta do GetCompress é simples, trocar, “processar um H×W gigantesco cheio de vazio” por “processar só o que está ocupado”, mantendo um contrato que permite reconstruir o grid original sempre que necessário.

Vale reforçar que aqui não estamos falando de compressão por entropia, como LZW e DEFLATE. O foco é compressão estrutural, isto é, remover o vazio do espaço e trabalhar apenas com pixels válidos. Em cenários com muito nodata, o ganho costuma aparecer de forma imediata.

Começamos pelo básico, organizamos os imports, definimos um valor de NoData de saída e escolhemos uma opção importante, se NaN deve ser tratado como NoData. Essa decisão do NoData de saída parece pequena, mas evita ruído em produção. NoData como NaN em GeoTIFF pode atrapalhar ferramentas e operações simples, enquanto 0 tende a ser mais previsível quando publicamos um produto binário, como máscaras e limiares (thresholds).

Antes de aplicar a compressão, garantimos que o stack esteja coerente e bem alinhado. Uma inspeção visual rápida no início do fluxo costuma evitar retrabalho quando há desalinhamento, truncamento ou padrões inesperados de NoData. Por isso, criamos duas rotinas simples: uma para exibir um raster 2D e outra para exibir um stack, limitando a visualização a até quatro bandas para manter a checagem objetiva e rápida.

Com essas funções, passamos a ter um sanity check do pipeline. Se surgir uma banda deslocada, uma faixa inteira zerada ou um recorte incorreto, ajustamos o problema antes de gerar a máscara, empacotar e salvar os artefatos.

O que nós chamamos de pixel ocupado

Agora definimos a regra que decide quais pixels entram no empacotamento. Aqui usamos uma abordagem pragmática e adequada para stacks multibanda: um pixel é considerado ocupado se pelo menos uma banda tiver valor válido. Assim evitamos perder informação útil quando uma das bandas tem falhas pontuais.

Para construir a máscara, combinamos duas noções de vazio. A primeira é a presença de NaN, comum em rasters de ponto flutuante. A segunda é um NoData explícito, quando o arquivo define um valor sentinela no metadado. A partir disso, reduzimos o stack a uma máscara 2D aplicando o critério “existe ao menos uma banda válida”. Assim, garantimos que o conjunto de pixels selecionado seja único e consistente para todas as bandas, evitando discrepâncias entre canais durante o processamento.

Empacotamento denso e o contrato de reversão

Com a máscara em mãos, realizamos a compressão estrutural. O objetivo é empacotar os valores válidos em uma grade densa quase quadrada e, ao mesmo tempo, guardar um contrato de reversão que permita reconstruir o grid original sem ambiguidade.

Esse contrato é o idx, um vetor de índices lineares do grid original. Na prática, ele é o mapa que liga o domínio comprimido de volta ao domínio espacial original. A partir dele, o custo de CPU e RAM passa a ser proporcional a N, que é a quantidade de pixels ocupados, e não a H×W do raster inteiro.

No empacotamento, começamos extraindo os índices onde a máscara é verdadeira e calculamos N, o número de pixels válidos. Em seguida, definimos a largura e a altura do contêiner denso, alocamos um array preenchido com NoData e copiamos para ele apenas os valores válidos, em ordem row-major. Por fim, registramos no metadado todas as informações necessárias para reverter a compressão e reconstruir o grid original.

Com isso, o custo de CPU e RAM passa a crescer proporcionalmente a N, e não ao produto H×W, evitando processamento desnecessário sobre grandes regiões vazias.

Descompressão para voltar exatamente ao grid original

Aqui fechamos a simetria do método com a descompressão. Essa etapa é o teste de sanidade mais importante, porque valida o contrato. Precisamos conseguir voltar ao shape original e reposicionar cada valor exatamente onde ele estava no grid original.

O processo é direto. Se o packed vier como (H, W), promovemos para (1, H, W). Em seguida, linearizamos o packed por banda e copiamos os primeiros N valores para as posições originais indicadas por idx. Todo o restante do grid recebe nodata_out, que costumamos definir como 0 quando o produto final é binário.

I/O para manter o pipeline reproduzível

Com as funções centrais prontas, organizamos o I/O para manter o pipeline reproduzível. Fazemos a leitura com rasterio, retornando array, profile, nodata e transform. Na escrita, atualizamos o profile com count, height, width, dtype e nodata, garantindo que o arquivo final fique consistente.

Também tratamos o metadata como artefato de primeira classe. É ele que sustenta o contrato de reversão. Por isso, salvamos meta em JSON e, no carregamento, reidratamos idx para um array numérico. Esse cuidado evita que idx vire uma lista comum e degrade desempenho quando voltamos a indexar.

Aplicando no caso com vento em múltiplas alturas

Com tudo pronto, realizamos o fluxo completo com um stack de vento em cinco alturas. Primeiro definimos um shape de referência para garantir consistência entre as bandas. Selecionei algumas coordenadas métricas bem na borda para ficar didático. Em seguida, lemos os TIFFs, recortamos todos para o mesmo shape e empilhamos no eixo de bandas.

Dimensões (5, 3600, 5400)

Antes de comprimir, visualizamos as bandas para validar alinhamento e padrões de NoData. Essa checagem reduz o risco de empacotar um problema que só apareceria depois, quando o custo de corrigir já ficou maior.

Compressão, salvamento e validação da ida e volta (round-trip)

Agora executamos a compressão estrutural. Geramos o packed e o meta, confirmamos o shape do contêiner denso e salvamos os artefatos. Em seguida, rodamos a validação de ida e volta, descomprimindo o packed e verificando que o shape original foi reconstruído corretamente.

Comprimido: (5, 2570, 2570) Meta: {'H': 3600, 'W': 5400, 'C': 5, 'idx': array([ 3925721, 3925724, 3925725, ..., 19439997, 19439998, 19439999]), 'N': 6602519, 'h': 2570, 'w': 2570, 'nodata': nan}

Restaurado: (5, 3600, 5400)
{'H': 3600, 'W': 5400, 'C': 5, 'idx': array([ 3925721,  3925724,  3925725, ..., 19439997, 19439998, 19439999]), 'N': 6602519, 'h': 2570, 'w': 2570, 'nodata': nan}

Operamos no comprimido e descomprimimos

A partir daqui, seguimos um padrão pronto para produção: carregamos o array comprimido junto com o metadado, reidratamos os índices (idx) e passamos a operar diretamente no domínio denso. Isso reduz o custo de varredura e acelera operações simples, como limiares (thresholds), filtros e combinações de máscaras, especialmente quando o grid original contém grandes áreas vazias.

Ah João, consigo colocar isso em produção?

Sim. A ideia é justamente essa: você salva a imagem comprimida e o artefato de metadados (com o contrato de reconstrução). Depois, quando precisar voltar ao formato original, basta usar esse meta para descomprimir e reconstruir o raster no mesmo grid, preservando forma, alinhamento e NoData.

João, dá para operar diretamente no raster comprimido e só descompactar no final?

Sim, e é exatamente esse o ganho do fluxo. Vamos fazer um teste com uma operação simples e comum: um limiar binário na banda de 100 m. Primeiro selecionamos a banda, definimos o limiar e criamos uma máscara de validade no domínio comprimido. Em seguida, aplicamos o limiar e produzimos uma máscara 0/1. Por fim, descomprimimos apenas o resultado binário para retornar ao grid original, já que é esse produto final que será publicado.

Tendo o nosso resultado comprimido, o arquivo meta e o NoData definido, é só usar a decompress_raster e realizar o processo reverso.

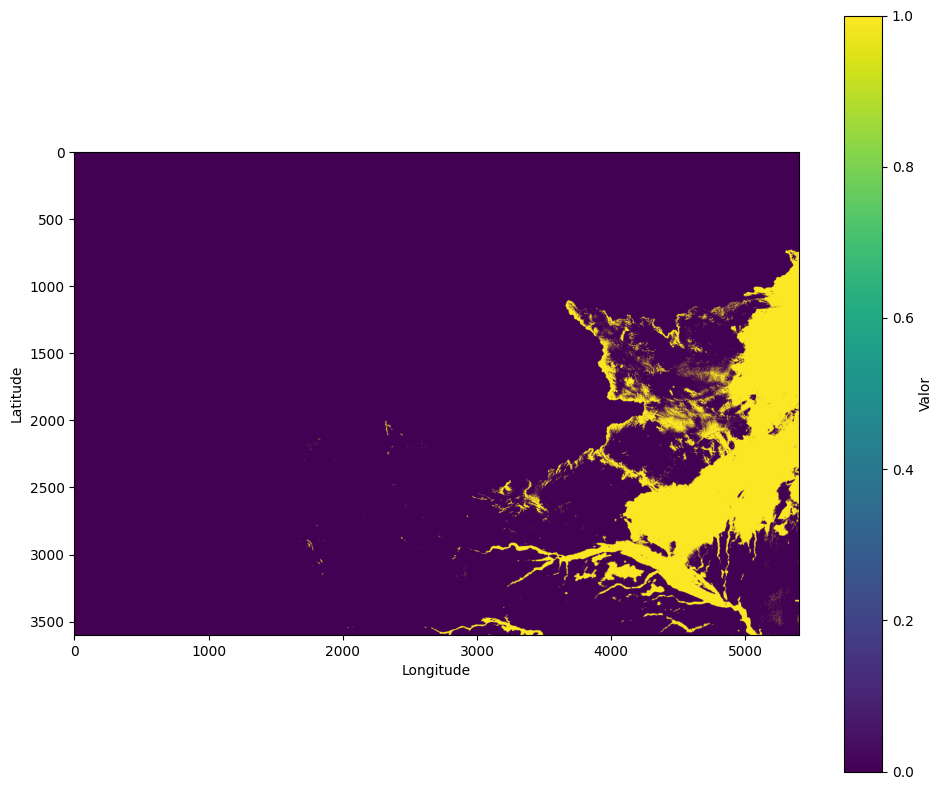
João, mas qual é a vantagem real em uso de memória? Vamos comparar.

Agora avaliamos o custo em RAM para entender onde o método “se paga”. Para evitar confusão, separamos claramente os conceitos. O stack original representa o custo cheio, proporcional a H×W (em todas as bandas), incluindo grandes áreas vazias. O comprimido representa o domínio denso, onde o custo passa a ser proporcional a N (apenas os pixels válidos), e é nele que as operações ficam mais baratas. Já o restored existe apenas para validar o contrato de reconstrução, por isso volta a ter o mesmo custo do stack original, pois reidrata o grid completo H×W.

stack: 370.79 MB, shape=(5, 3600, 5400), dtype=float32
compressed: 125.98 MB, shape=(5, 2570, 2570), dtype=float32
packed: 370.79 MB, shape=(5, 3600, 5400), dtype=float32

O que essa comparação mostra, de forma bem direta, é a diferença entre operar no domínio cheio e operar no domínio denso. Ao sair de 370,79 MB para 125,98 MB, o domínio comprimido reduz o consumo de RAM em aproximadamente 66,0%. Em outras palavras, o comprimido passa a usar cerca de 34,0% da memória do stack original, e é essa redução que se traduz em varreduras mais baratas e operações mais rápidas no dia a dia.

Em produção, além do array comprimido, o item que realmente define o custo do contrato é o idx. É ele que permite reconstruir o grid original, então precisa ser armazenado e carregado com eficiência. Quando idx é salvo como lista em JSON, o arquivo pode crescer muito por overhead de serialização. Por isso, costumamos separar metadados pequenos do vetor grande.

O caminho mais direto para reduzir custo é armazenar idx em um tipo menor quando isso for possível. Como o índice linear máximo é H×W, se esse valor couber em uint32, podemos reduzir o custo do idx pela metade em comparação com int64. Quando também compactamos o arquivo binário, muitas vezes o ganho aumenta ainda mais, dependendo da estrutura do índice.

Quando faz sentido, também podemos armazenar a máscara de ocupação em vez do idx. A máscara ocupa H×W bits e pode ser bem menor em disco. O trade-off é que, na carga, precisamos reconstruir idx com uma operação de flatnonzero, o que adiciona um passo no carregamento, mas mantém o contrato funcional.

Fechando o pipeline do jeito que vira produção

No fim, o que construímos com o GetCompress é uma representação intermediária que reduz custo de computação sem perder rastreabilidade. Comprimimos uma vez, operamos várias vezes no domínio comprimido e descomprimimos apenas quando precisamos publicar um produto no grid original.

O cuidado principal é não tratar o packed como um raster espacial. Ele é um contêiner. Quem garante integridade é o meta, então tratamos esse metadata como artefato de primeira classe: versionamos junto, validamos consistência entre N, idx e H×W, e escolhemos um formato de persistência que não estrangule o ganho do método.

Quando seguimos esse padrão, limiares, máscaras, filtros e estatísticas deixam de varrer um H×W gigante cheio de vazio e passam a operar no conjunto de pixels que realmente importa. Isso melhora desempenho e simplifica o fluxo de produção sem abrir mão do grid original.

Referência

ALMAGHRABI, Sarah; RANA, Mashud; HAMILTON, Margaret; RAHAMAN, Mohammad Saiedur. Multivariate solar power time series forecasting using multilevel data fusion and deep neural networks. Information Fusion, v. 104, art. 102180, 2024. DOI: 10.1016/j.inffus.2023.102180